In this lesson, we shall learn how to work with trigonometric functions. The three basic trigonometric functions are sin, cos and tan which stand for sine, cosine and tangent. We also deal with the inverse of tangent, Atn.
The sin function returns the sine value of an angle. We need to convert the angle to radian as Excel VBA cannot deal with angle in degree. The conversion is based on the following equation:
π radian= 180o
so 1o=π/180 radian
The issue is how to get the exact value of p? We can use p=3.14159 but it will not be accurate. To get exact value of π, we use the arc tangent function, i.e. is Atn. Using the equation tan(π/4)=1, so Atn(1)=π/4, therefore, π=4Atn(1)
The syntax of the Sine function in Excel VBA is
sin(Angle in radian)
In this example, we use pi to represent π and assign the value of π using the formula pi = 4*.Atn(1). We use the function Round the value of sine to four decimal places.
Private Sub CommandButton1_Click()
Dim pi As Single
pi = 4*.Atn(1)
MsgBox("Sin 90 is" & Round(sin(pi/2), 4))
End Sub
Running the program produces the message as shown in Figure 7.1

The cos function returns the cosine value of an angle
The syntax of the Cos function in Excel VBA is
cos(Angle in radian)
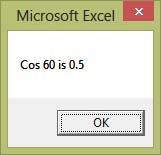
Private Sub CommandButton1_Click()
Dim pi As Single
pi = 4*.Atn(1)
MsgBox("Cos 60 is" & Round(Cos(pi/3), 4))
End Sub
Running the program produces the message as shown in Figure 7.2
The tan function returns the tangent value of an angle
The syntax of the tan function in Excel VBA is
tan(Angle in radian)
Private Sub CommandButton1_Click()
Dim pi As Single
pi = 4*.Atn(1)
MsgBox("Tan 45 is" & Round(tan(pi/3), 4))
End Sub
Running the program produces the message as shown in Figure 7.3

Copyright ® 2008 Dr.Liew Voon Kiong . All rights reserved [Privacy Policy]
Contact: Facebook Page