[Lesson 6]<<[Table of Contents]>>[Lesson 8]
Mathematical functions are very useful and important in Excel 2010 VBA programming because very often we need to deal with mathematical concepts in programming such as chance and probability, variables, mathematical logic, calculations, coordinates, time intervals and etc.
The common mathematical functions in Excel 2010 VBA are Int, Sqr, Abs,
Rnd is very useful when we deal with the concept of chance and probability. The Rnd function returns a random value between 0 and 1. In Example 7.1. When you run the program, you will get an output of 10 random numbers between 0 and 1 each time you click on the OK button of the message box.
Example 7.1
Private Sub CommandButton1_Click() For x = 1 To 10 MsgBox Rnd Next x End Sub
Random numbers in its original form are not very useful in programming until we convert them to integers. For example, if we need to obtain a random output of 6 random integers ranging from 1 to 6, which make the program behave as a virtual die, we need to convert the random numbers using the format Int(Rnd*6)+1. Let’s study the following example:
In this example, Int(Rnd*6) will generate a random integer between 0 and 5 because the function Int truncates the decimal part of the random number and returns an integer. After adding 1, you will get a random number between 1 and 6 every time you click the command button. For example, let say the random number generated is 0.98, after multiplying it by 6, it becomes 5.88, and using the integer function Int(5.88) will convert the number to 5, and after adding 1 you will get 6.
Example 7.2
Private Sub Commandbutton1_Click ( ) Num=Int(Rnd*6)+1 MsgBox Num End Sub
Now, run the program and then click on the button, you will get an output of number 1 to 6 randomly display on the message box.
b) Int is the function that converts a number into an integer by truncating its decimal part and the resulting integer is the largest integer that is smaller than the number. For example, Int(2.4)=2, Int(4.8)=4, Int(-4.6)= -5, Int(0.032)=0 and so on.
c) Sqr is the function that computes the square root of a number. For example, Sqr(4)=2, Sqr(9)=2 and etc.
d) Abs is the function that returns the absolute value of a number. So Abs(-8) = 8 and Abs(8)= 8.
e) Exp of a number x is the value of ex. For example, Exp(1)=e^1 = 2.7182818284590
f) Fix and Int is the same if the number is a positive number as both truncate the decimal part of the number and return an integer. However, when the number is negative, it will return the smallest integer that is larger than the number. For example, Fix(-6.34)= -6 while Int(-6.34)=-7.
g) Round is the function that rounds up a number to a certain number of decimal places. The Format is Round (n, m) which means to round a number n to m decimal places. For example, Round (7.2567, 2) =7.26
g) Log is the function that returns the natural Logarithm of a number. For example,
Log (10)= 2.302585
Example 7.3
Private Sub CommandButton1_Click() For i = 1 To 10 MsgBox Sqr(i ) Next End Sub
This program will find the square root of number 1 to 10 and displays them on the message box each time you click on the OK button.
Example 7.4
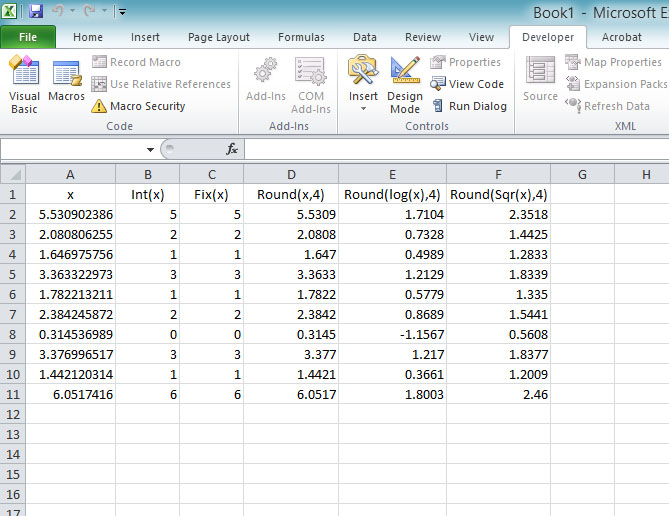
In this example, we created an Excel 2010 VBA to compute the values of Int(x), Fix(x), Round(x,4) and Log(x) and displays them in respective cells. Notice that you can combine two or more functions in your code, like Round(Log(x)). It uses the Do Loop statement and the Rnd function to generate random numbers. The statement x = Rnd * 7 generate random numbers between 0 and 7 . Using commas in between items will create spaces between them and hence a table of values can be created. The program is shown below and the output is shown in Figure 7.1:
Private Sub CommandButton1_Click() Dim n As Integer Dim x As Single n = 2 Do While n < 12 x = Rnd * 7 Cells(n, 1) = x Cells(n, 2) = Int(x) Cells(n, 3) = Fix(x) Cells(n, 4) = Round(Cells(n, 1), 4) Cells(n, 5) = Round(Log(x), 4) Cells(n, 6) = Round(Sqr(x), 4) n = n + 1 Loop End Sub
Figure 7.1
<br />
(adsbygoogle = window.adsbygoogle || []).push({});<br />